Common property owned simultaneously by several persons is considered shared property. For example, a husband and wife bought a new apartment and incurred equal costs, and therefore the documents reflected the fact that 50% of the real estate is the property of each family member.
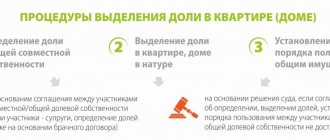
There are two options for allocating part of the property. The first of them does not violate the principles of common property. Having formally received rights to part of the property, you will not be able to dispose of it without the permission of the other co-owner. But allocating a share in kind allows you to dispose of your part of the property. The owner can sell the share of the home or receive compensation for it from the co-owners.
You can allocate shares and record the fact of shared ownership using an agreement. In this case, the parties agree and decide how to correctly allocate parts of the common property, and then write down all the details in the document, sign it and notarize it.
However, in practice there are cases when it is not possible to reach an agreement, which means that the conclusion of a peace agreement is cancelled. Then questions about the share of common property are resolved with the help of the court. You need to prepare your arguments well and collect a high-quality evidence base. A professional lawyer can help you with all this, as well as in drawing up a statement of claim. Family and housing disputes are most often complex and conflict-ridden, so choose a specialist who will defend your interests in court.
New law on microshares
The bill is aimed against so-called raiders who register ownership of micro-shares and then survive the current owners. There are cases when people were left homeless or were looking for money to buy out microshares. The introduction of amendments should limit fraudulent schemes.
The initiative was submitted for discussion to the State Duma on December 21, 2017. The bill has already passed the first reading and amendments are being prepared. However, it is too early to talk about its application - as of the first half of 2021, it has not yet entered into legal force . However, courts use some of the sentences when making their verdicts.
The main essence of the law on microshares:
- a ban on their sale to strangers;
- restriction in registration (registration) if the share does not correspond to the minimum housing standard per person (from 8 to 15 m²);
- a ban on moving into an apartment if the owner’s share is less than the accounting norm (footage).
An exception would be the splitting of an apartment into microshares as a result of privatization or inheritance.
Expert opinion
Makarov Igor Tarasovich
Legal consultant with 8 years of experience. Specialization: criminal law. Extensive experience in document examination.
Grandmother owns a room in a communal apartment. A pensioner wants to leave her home to her grandchildren. The problem is that there are 5 grandchildren. If the inheritance opens, the room will be divided among all the grandchildren.
Each of them will receive 1/5 of the share, i.e. microlobe.
According to the new law, such a division does not pose any problems, since there is a family connection.
The 3-room apartment belongs to four owners. One of them wants to split the ¼ share into 2 parts - keep ⅔ for himself and sell ⅓ to his friend.
However, the buyer is not a family member and is not listed as a relative of any of the occupants. If previously it was possible to purchase a third ¼ share and take possession of 1/12 of the housing, the new law will limit such fragmentation.
Considering that 1/12 in a 3-room apartment is a micro-share, the transaction will not take place. The new owner will not be able to live in the apartment, since part of it is less than the housing registration norm - 8-10 m².
How to determine the share size
Becoming the owner of a share is possible only under a division agreement with the help of a court decision, as well as under the terms of shared ownership, which are established at the time of purchase of the property. If your case does not fall under any of the above, then you are one of the owners of common property.
This means that you have some share, but you do not know its size and it is not documented in any way. How, then, can you find out the size of your share of the property?
The owners' shares in common property are equal by default. For example, an apartment measuring 60 sq.m. three owners. So, each owner by default owns ⅓ of the apartment, that is, 20 sq.m. But how to divide the shares so that it is possible to dispose of, for example, a separate room?
Article 252 of the Civil Code of the Russian Federation allows for the determination of a share in kind, but stipulates a number of conditions, the main one of which is the continued suitability of the property for citizens to live in it. For example, it is impossible to physically divide a one-room apartment into two separate living spaces, equip separate entrances, divide or move communications, cut a window in a load-bearing wall for a second room - that is, carry out a full-scale redevelopment. Therefore, it will not be possible to divide such housing.
But if the apartment is large enough, it has several separate rooms, it is technically possible to refurbish it, make separate entrances - separating it is quite possible. The condition for carrying out such a procedure will be the approval of the redevelopment by local authorities and the registration of two separate technical passports in the BTI.
In some cases, a complete division of one living space into two (or more) separate ones is technically impossible, even if it is quite spacious. In such cases, the law allows co-owners to transfer the apartment to communal status. Each co-owner will have personal ownership of the room in which he will live, and common areas (kitchen, bathroom, corridor) will remain common.
By maternity capital
Purchasing housing using maternity capital requires allocating shares to mom, dad and children. It is important to ensure comfortable living in the apartment. Therefore, the law has a clear requirement to allocate children a share that corresponds to the minimum living standard.
Parents may not allocate equal percentages to themselves and their children. It is rational to calculate the size of shares in proportion to the amount of capital. See what part of the monthly rent was spent on buying an apartment. From here you can secure the children's and adult parts in the living space and conclude an agreement on determining the shares.
Share in an apartment purchased with maternity capital.
Maternity capital is a targeted payment that can be used to improve living conditions. If it is used to purchase an apartment, then shares must be allocated for each family member, including minor children.
However, the law does not specify the size of the part. The minimum share of an apartment for maternity capital is usually determined in proportion to the value of the property and the invested funds.
The size of the parts is specified in the agreement, which is certified by a notary.
It must be taken into account that if the guardianship authorities consider that the interests of minors have been violated, the transaction can be annulled in court.
In this case, the parents will be required to return the funds to the Pension Fund.
Allocation of shares to children when using maternity capital: cost, documents.
For accommodation
The desire not only to register, but to live in an apartment, presupposes a minimum share in the property. The calculation is carried out depending on the size of the apartment:
- 4-room or 3-room – at least ¼ of the share in the common law (room);
- 2-room – ½ apartment ;
- 1-room, studio or small family - entirely (with the exception of spouses, parents and children).
Expert opinion
Makarov Igor Tarasovich
Legal consultant with 8 years of experience. Specialization: criminal law. Extensive experience in document examination.
The minimum allowable standard for one person to live is 6 m². This area is allocated in dormitories, service apartments and flexible housing.
For registration (registration)
Not everyone wants to own a share and live in an apartment at the same time. There are people who would be satisfied with registration at the place of registration of property rights. For example, to register for school, kindergarten, employment, receive medical and social assistance, and apply for a pension.
However, more and more courts are refusing to allow plaintiffs to register for meager shares . Explanation: the latter do not correspond to the minimum housing standard per person.
Our family wants to buy a share in an apartment for the purpose of registration in it. Tell me, what should be the minimum size of this share? One seller offers us 3 m², and the second one offers us 1 m². Can the local Federal Migration Service refuse registration in such an area, and are there any standards at all?
Currently there are no specific parameters for the area for registration (registration) of citizens. The law determines the minimum housing standard per person – 12 m², but these indicators differ in the regions.
It is recommended to buy shares that can be represented as isolated premises. If you buy such a room, there will definitely be no problems with registration.
At the same time, you will be able to live in the room. There is no point in purchasing 1 or 3 m² just for registration. Focus not on the “squares”, but not on the actual living space. Thus, you will avoid the risk that the remaining co-owners will buy out your meager portion.
Registration of a minor
Registration of a share in the living space of a minor child is possible without the consent of the other owners, subject to the condition of living together with the latter. It will not work to purchase part of the living space only for the permanent or temporary registration of a child or children.
Permanent registration of a third party requires notification and a positive decision of all property owners. To register at a new place of residence, you must register with the Federal Migration Service within a week from the date of arrival. Registration is completed within three days after submitting the application, with a new mark being placed in the passport.
For rent (hire)
Is it possible to rent out a minimum share of an apartment?
If the size meets the requirements of the Housing Code of the Russian Federation, there will be no problems with renting out. The main condition is isolation of the living space . For example, it could be a living room: living room, bedroom, etc.
The second point is the consent of the remaining co-owners . If the share is not allocated in kind, their consent is required. You cannot rent out a room without the permission of the owners, otherwise they may file a lawsuit and invalidate the transaction.
Read more about all the issues with rent in the article “Renting out a share in an apartment without the consent of the owners.”
How to calculate the minimum share?
So, we figured out that the minimum share corresponds to the accounting housing area per person. It remains to figure out how to carry out arithmetic calculations of fractions.
Zhn – housing standard in accordance with the Housing Code of the Russian Federation (example: ⅓ part of 30 m²).
We have an apartment with a total area of 80 m². Let's determine the share that allows you to both live and register in the living space:
80 m² from 1/10 of the permissible norm, i.e. 80 / 10 = 8 m² per person.
The indicator is calculated based on living space (rooms). Non-residential parts of the apartment and house are not included here. Co-owners have equal rights to use them. Read more about calculations in the article “How to calculate the share in the right of common ownership of common property?”
Legal mathematics, shares, fractions, proportions.
I have long wanted to write something on legal mathematics. I noticed that many colleagues underestimate mathematics, but in vain. I believe that a lawyer would simply be nowhere without it, and if it were up to me, I would teach a special course in legal mathematics in universities when teaching law students. This, I believe, is the first article on this topic. To the best of my ability, I will try to introduce different options for legal calculations in different cases, but first about fractions. Fractions are an inheritance, and, as they say, “in inheritance law, all jurisprudence is reflected, just as the entire sea is reflected in a drop of water.” Why does a lawyer need mathematics and why does a lawyer need to know operations with fractions? Try to solve the following problem first: Heirs A. B. C. G. and D. each received an inheritance according to the will: A. – 1/8 of the testator’s property; B. – 6/17; V. – 3/123, and everything else was bequeathed to D.’s heir. However, citizen I intervened, having the right to an obligatory share in the inheritance, while the share that would have been due to her by law was 1/6, respectively, she received 1/12 from this inheritance. What shares now went to each of the heirs A. B. C. G. and D. if we reduce them by the shares that went to citizen I? For interest, I will inform you that the share of the last heir D. became 7009/16728.
In Russian there is an expression “to get into trouble”, in German there is a similar expression “to get into fractions”. In operations with fractions, you can easily end up in a very complicated situation; it’s very easy to make a mistake, but we know what a lawyer’s mistake costs. And here a screen like phrases like “notaries or civil lawyers need this, but we, criminal lawyers, don’t need it” will not help.
Imagine that in the above example, one of the shares is the subject of a crime and it is necessary, in relation to the value of the inherited property, to determine whether the damage is large or especially large? And it’s somehow embarrassing for a lawyer, when a client comes to him, to demonstrate a complete inability to calculate fractions.
Fractions are needed everywhere and always, whether we count percentages, calculate the weight of goods, determine taxes, or divide property. In many, many questions you cannot do without fractions.
Below are practical problems that demonstrate the need for mathematical operations with fractions and their knowledge. You will find answers to the problems via the links if you click on them. But don’t rush to look at the answers, try to decide for yourself. I believe that after reading the article, it will not be difficult for you to do this and once will be enough forever. Actions with fractions. Adding and subtracting fractions. It is easiest to add and subtract fractions if they have the same denominator. In this case, the numerators are added or subtracted and give a result with the same low denominator.
Let's try to imagine this visually. We have a pie cut into 7 pieces. Masha was given 3 pieces on a plate, Petya was given two pieces, and Vitya was also given two pieces. Vitya ate his part, and Masha and Petya left their parts. How many pieces are left? This simple example shows why the denominator remains the same. Similarly with subtraction, with the same denominator it is not difficult to do.
In general:
What if the denominators are different? Then, it is necessary to reduce the fractions to the same denominator. The easiest way to do this is to sequentially multiply fractions by each other, starting with fractions that have fewer digital signs and moving on to increasingly larger ones.
Here the fraction 2/5 had to be converted into the fraction 4/10. There is nothing wrong with this, because if we imagine a pie cut into five parts, we take 2 parts from this pie, then we will notice that if we cut the same pie into 10 parts and take 4 parts, then the size will be 4/10 equal to the same 2/5. That is, we are dealing with the same fraction.
There are fractions that are very large in the number of signs, and therefore, when bringing them to a common denominator, it is advisable to find a smaller factor. In the example below, it seems that the smaller fraction is being subtracted from the larger fraction, but in fact it’s the other way around, which is why the result comes out as a negative number (that is, there is a shortage of pieces of the pie.)
Let's complicate the examples a little.
Again, by multiplying the numerator and denominator, we reduce the fractions to equal ones. Only, pay attention, due to the fact that the fractions are inconvenient, we had to multiply the left fraction and the numerator and denominator by the denominator of the right one, and the right fraction by the denominator of the left one.
When performing operations with multiple fractions, you need to find the denominator common to all fractions and reduce each fraction to this same denominator.
If we multiply 2, 4, 8, and 16, we get the denominator 1024. You can operate with it, but you can simply find that the number 16 is divisible by 2, and 4, and 8. And if so, by multiplying it’s easy from the numbers 2, 4, 8 we get the number 16. If we multiply the denominator 2 by 8, then we multiply the numerator by 8 so that the overall proportion within the fraction is preserved. Indeed, if we take only 8 parts from a pie cut into 16 parts, we will find that this is exactly half of the pie, that is, 1/2 of it. The fraction 3/4, when multiplied by 4, becomes 12/16. The fraction 7/8 is converted to 14/16 by multiplying by 2. As a result, solving this example should result in 29/16. It is possible to solve this example with a denominator of 1024, but such a solution will be cumbersome. Multiplying and dividing fractions is much easier. To multiply a fraction by a fraction, you multiply the numerators (this will be the numerator of the result) and the denominators (this will be the denominator). The general formula is:
For example:
Just in case, I note that there is no need to look for a common denominator here. As you know, to multiply means to repeat the addition of what is being multiplied as many times as the number of the multiplier requires. So 2 multiplied by three means 2+2+2, that is, three times. Same with fractions, 2/3 multiplied by 3/4 means that two parts of a pie cut into three pieces must be repeated several times. As a result of this repetition we get 6/12. This result must be reduced by dividing both the denominator and numerator by 6, resulting in 1/2. Did you notice? It seems like they multiplied 2/3, which is more than half, but in the end they got half! Because multiplying by a fraction means dividing. After all, the fraction itself is a “frozen division”.
Try multiplying 2 by 1/3, what do you get? It turns out 2/3. And indeed 2 can be represented as a fraction 2/1, then it will be 2/1 * 1/3. We multiply the numerator by the numerator, and the denominator by the denominator and get 2/3. In fact, we took two whole pies and cut off 1/3 from each of them, so we ended up with 2/3. Obviously, multiplying by a fraction actually means dividing. But we know that division is the inverse operation of multiplication. So, with fractions, when we do division, we actually get multiplication?
Let's see if this is so, but first you just need to remember the rule for dividing a fraction by a fraction: To divide a fraction by a fraction, you need to simultaneously change the sign of division to multiplication and “turn over” the second fraction, put the numerator in place of the denominator, and the denominator in place of the numerator.
For example:
Why does multiplication occur here? The concept of dividing a fraction by a fraction is difficult for humans to formulate, apparently for this reason, in Ancient Egypt, mathematicians preferred to deal with fractions in the form 1/n. To do this, all other fractions were reduced to this form, for example, the fraction 3/4 was reduced to the form 1/2 + 1/4. These fractions are easier to operate with and easier to understand. The fact is that, as mentioned above, division is the inverse operation of multiplication. So the operation 2: 2 can be written as 2/2, or 2 * 1/2. The operation 12:4 can be written as 12/4. But you can imagine it differently than 12……. 4 — : —- 1……… 1 Now pay closer attention! “Turn over” the second fraction and...!!! We come to the form 12/4 12……. 1 — * —- = 12/4 1……… 4 For this reason, when dividing a fraction by a fraction, the fraction that is the divisor is “turned over.”
We didn’t notice this feature right away. Initially, when they counted with the help of an abacus, they tried to reduce the fraction to a whole number, then, in the interests of addition and subtraction, they began to reduce fractions to a common denominator. As a result, we came to the conclusion that the operation of equalizing fractions is unnecessary. Initially, division was carried out according to the following procedure: a/b: c/d = ad/bd: cb/bd = ad/cb. For example: 2/3: 4/5 = 2*5 / 3*5: 4*3 / 5*3 = 2*5 / 15 : 4*3 / 15 – as a result, the denominator “15” can be removed and we get – 2*5 / 4*3 = 10/12 = 5/6 The last expression “2*5 / 4*3” is essentially equal to “2/3 * 5/4”, see for yourself:
Notice how the second fraction, the divisor, “turned over”? From here, even in ancient times, it became obvious that reduction to a single denominator did not give anything, and you can shorten the calculations by simply turning over the second fraction. Suppose we have half a round pie, or 1/2 of it. Let's assume that there is a plate with the same diameter as this round pie. But in fact, we saw this plate into 4 parts and we only have 2 such quarters, or 2/4. How to divide 1/2 of a pie into 2/4 of a plate? But there’s no way, half a pie simply won’t fit 1/4. Therefore, you will have to take and add the second quarter, then there will be half a plate, and on it half of the pie of the same diameter. As a result, 1/2 of the pie will fit exactly on 2/4 of the plate. But this turns out to be a whole circle in diameter! It turns out that if 1/2: 2/4 = 1 Let’s check by inverting the second fraction: 1/2 * 4/2 = 4/4 = 1
That's right, that's how it is. The numbers are ideal, and we are not interested in whether the circle or its parts are a pie or a plate; what is important is that as a result of dividing a fraction by a fraction, we get a whole, in a numerical ideal, circle, so to speak, in assembled form. By the way, in ancient times they reasoned in a similar way, only they divided shares of the profit between people, and they did not hesitate to represent people as, for example, “three-quarters of a person.” But these arguments are complicated, I will not give them. If anyone is interested in practicing logic, judge for yourself. It's interesting to look at the division operation when we deal with decimals. So division 4: 0.5 means 4/1: 5/10. But the second fraction needs to be reversed and we get: 4/1 * 10/5 = 40/5 = 8 Since we know that 0.5 is the same as 1/2 (reducing 5/10, we divide the numerator and denominator by 5 , and we get 1/2), then you can do it simply, as soon as we see 4: 0.5, immediately just double the four = 4 * 2 = 8 And if 4: 0.3 then how to multiply? Yes, and multiply, if when dividing by 0.5 we got 40/5, then here we get the same 40/3. In this case, the number 40 fits 13 numbers 3 and another 1/3 remains. Therefore, we bring the improper fraction to the normal form ...... ...1 13 - ...... ...3 40 = 30+10 = 30 + 9 + 1 = 10*3 + 3*3 + 1 = 13 “pieces” of triplets and the number “1” in the remainder, which will become the numerator in the improper fraction. What if 4: 0.03? Since this is three hundredths, we get 4 hundredths in the numerator and a three in the denominator, or an improper fraction of the form 400/3. Let's bring it to normal form and get: ...... ...1 133 - ...... ...3 And so on, similarly. By the way, decimal fractions with hundredths and percentages are the same thing. See for yourself: 0.5 = 0.50 = 50% 0.25 = 25% 0.8 = 0.80 = 80% 1 = 1.00 = 100% Here, if necessary, simply add a zero and move the decimal place two places. Let’s take it more complicated: 0.1567 = 15.67% That is, as in the above examples, we simply move the decimal point two places to the left. Therefore, finding the percentage of a number is extremely simple; you just need to multiply by the fraction. How to find 50% of the number 4? It’s simple, because 50% is 0.5 or 1/2 Then 4 * 1/2 = 4/2 = 2 How to find 25% of 84? And it’s also simple: 84/4 = 41 Proportions. Well, I really love proportions, they can be considered anything, and the change in volume depending on the change in temperature, and the height of a skyscraper along the length of its shadow, and much, much more. To demonstrate the full power of the method of proportions, I will give a well-known historical example: The ancient Greek philosopher, scientist and prominent political figure Thales of Miletus (625 - 547 BC) was one of the first (except for the Chinese scientists who knew everything about fractions and proportions in the 2nd century BC) came to the conclusion about the proportionality of the sides of similar triangles.
He knew how to find any unknown quantity from three known ones based on the proportion a/b = c/d. Thus, having measured the length of the shadow cast by objects, Thales, using this proportion, found the height of the Egyptian pyramid. He also measured the distance to a ship located far out to sea based on this proportion. Having chosen a base A on the seashore and measuring the angles to the ship from its extreme points, he then drew a similar triangle of small dimensions and measured its two sides, say C and D. After this, it was easy to find the unknown distance to the ship - side B.
Now this is called the triangulation method, and it is used by all cadastral engineers (surveyors) when they run around with their theodolites, and then draw something on paper called an outline, these are just triangles. These triangles touching each other describe the land plot; with their help, the main distances are found and the areas are calculated.
The rule of proportion is applied if there is equality of two fractions: A………… C —- = —- B………… D According to the rules of equality of a fraction, when the denominator is transferred to the other side behind the equal sign, it goes into the numerator and if there is another numerator there multiplied by it. It's easy to verify this. Let's say we have an equality of fractions: 3/4 = 21/28 Then: 3 = 4*21/28 (to see what we have done, we can imagine it like this: 3/nothing = 4*21/28) or 21 = 3 *28/4 (to see what we have done, we can imagine it like this: 21/nothing = 3*28/4) If we move the numerator beyond the equal sign, then it goes into the denominator and is multiplied by the value that is already there. there is nothing/4 = 21/28*3 However, such an expression is unacceptable, because we will get “nothing from four parts” on the left side, that is, zero. Then move “4” to the right, behind the equal sign, and the numbers from the right side to the left. 28*3/21 = 4 Now everything is fine. Then you can do the same with the other part of the fraction. 3/4*21 = there is nothing/28 28 = 4*21/3 You can move both denominators to the other side, as a result we get: 3 * 28 = 21 * 4 check: 3*28 = 84 21*4 = 84 84 = 84 What did we get? But it turned out that the equality of fractions A………… C —- = —- B………… D Can be written in the form: A * D = C * B Or in the form: ………… C*B A = —- …………D………. A*D B = —- ………. C ………… A*D C = —- ………… B ………… B*C D = —- ………… A You can simply remember this rule: “multiplication is performed crosswise”: the numerator of the first fraction to the denominator of the second and vice versa. That is, if we have - with “A” there is a corresponding “C”, then - with “B” there will be a corresponding “D”. You can visualize: A - C. \/. / \ B – D The “cross by cross” rule will show that to find the unknown A you need to “cross by cross” take C, multiply it by B and divide by D ……… C*B A = —- ………. D Or, let’s say, we don’t know D. Then again “cross to cross” - take B, multiply it by C and divide by A. ……… B*C D = —- ………. A And the like... Why does this happen? Let's imagine that we cut one pie into 4 equal parts, and another similar pie was cut into 28 equal parts. Now, if we take 1/4 of the first pie and 7/28 of the second pie, we will get equal parts. Accordingly, if we take 2/4 from the first and 14/28 from the second – again equality. If we take 3/4 from the first and 21/28 from the second, we again get equal parts. If we need to determine which part of the second pie is equal to 3/4 of the first pie, then what do we do? (Imagine this visually and you will understand the rule of proportion for the rest of your life.) Correct. We mentally divide the 28 parts of the second pie into four parts and find that in each of the four parts we have 7 pieces. That is, 1/4 for a pie divided into 28 parts will consist of 7 pieces, or 7/28ths. Next, we will mentally take 7 pieces three times, and we will get 21. What have we done? We divided 28 by 4 and multiplied by 3. 28/4*3 = 21 In fact, we acted according to the rule of proportion, knowing that for “4” there is a corresponding “28”, then for “3” “there will be a corresponding “unknown number” Therefore, we “cross on a cross”: 28 * 3/4 (and got) = 21. Reversing the numbers during multiplication and division does not change the result: 28/4*3 = 28*3/4 = 3*28/4=3/4*28 – everything is the same. — Imagine dividing 28 parts of the pie into four and taking 3 of them. — out of 28 pieces of the pie, we took 3 out of 4. - they took 3 parts of the pie, when it was divided into 28 parts and they were divided into 4 parts. - took 3 out of 4 parts of the pie divided into 28 parts. All the same. Or if the fractions are equal 3/4 = 21/28, we transferred 28 beyond the equal sign and got 28*3/4=21 Where do we need the rule of proportion? And wherever in calculations it is necessary to determine the unknown, when it is known that there is equality of shares. For example, in percentage calculations. After all, a percentage is the same fraction that in its original state looks like 100/100. Let's say 10% is 10/100, and 50% is 50/100. When we say “50% of 1000 rubles,” we are talking about a proportion, indicating that 50/100, or 1/2, or actually 500 rubles are taken from 1000 rubles. Let's say. We know that there are 3,000 rubles borrowed. To use the loan you need to pay 3% per month. The loan was used for 4 months, that is, you must pay 12% of the loan amount (4 months * 3% per month = 12%). How much will it be in money? 3000 rub. corresponds to 100% - there is X rub. should correspond to 12% - there “cross to cross” we get:
3000 rub. * 12% ———————— = X rub. 100% X = 3000 * 12 / 100 = 360 rubles. Although, remembering that percentages and decimal fractions are the same thing, we can do it simpler: 3000 * 0.12 = 30 *12 = 360 But what about value added tax calculations? If, say, we know that an 18% tax was charged on the price of a product, which is unknown to us, and as a result the product was sold for 5,600 rubles (VAT is included in this amount)? How can I find the VAT amount here? Try to calculate for yourself what the price of the goods was (count, then read further). You should get: 4745.76 rubles. Did you get this amount? I guess it didn't work out. Those who got 4,592 rubles are wrong. My number is correct. Look for yourself, if you calculate 18% of 4745.76 rubles, and then add the calculated interest and the original price of 4745.76 rubles, you will get exactly 5600 rubles: 4745.76 rubles. corresponds to 100% - there is X rub. must correspond to 18% VAT We do “cross to cross”: X = 4745.76 * 18 / 100 = 854.24 rubles. VAT amount 4745.76 + 854.24 = 5600 rub. for which the goods were sold. My figure is correct, why were you wrong? I suppose you thought like this: 5600 rubles. corresponds to 100% X rub. corresponds to 18% X = 5600 * 18 / 100 = 1008 rub. VAT 5600 – 1008 = 4592 rubles But this is not true! Do you understand where the error is? “A tax of 18% was charged on the price of the goods” and... the goods were sold with this tax, “VAT is included in this amount.” And since it is included, we accepted the amount as 100%, then we charged VAT on it at 18%, then they added it and sold it for 118%!!!! 5600 rub. correspond to 118% there (not 100%) X rub. corresponds to 100% there X = 5600 * 100 / 118 = 4745.76 rubles We got the desired result. Now try to “extract” VAT from the amount of 5,600 rubles. 5600 rub. correspond to 118% - there X rub. corresponds to 18% there And? What happened? In the methodological literature, it is often proposed to isolate VAT from the amount in which it is included by multiplying by 0.15. In principle, this is close to the truth, because: 118% / 18% = 0.1525423728813... or rounded 0.15. In this case, we calculated the proportionality coefficient. So in our example, 3/4 = 21/28 = 0.75 is a single proportionality coefficient.
In principle, if we need to find out the numerator for a denominator of 28, we can simply multiply 28 by this coefficient of 0.75 and get the desired number 21. But with the calculation of VAT, this “trick” does not work, since jurisprudence intervenes here, and inaccuracy of calculations gives rise to legal risks. Look for yourself, with our sales amount of 5,600 rubles, VAT is 854.24 rubles.
And if we 5600 rub. multiply by a factor of 0.15, we get 840 rubles. That is, it turns out less than expected. This was due to rounding of the coefficient. When checking, the tax inspectorate will quickly find under-accrued VAT and impose a fine. In this example, a small figure is taken, but in the real work of enterprises there will be millions of sales, which from such a small inaccuracy will result in huge tax fines. Using the rule of proportion, we accurately find the required VAT amount. It is much more correct and accurate to calculate by proportions. Conclusion: You need to be careful when determining the corresponding parts of the proportion. You need to be especially attentive to the essence of proportion. The direct proportion was discussed above, but there is also an inverse one. Those discussed above were expressed as follows: - If with “A”, which is greater, there is a corresponding “C”, which is greater, - Then with “B”, which is less, there will be a corresponding “D”, which is less Or simply “more-more”, “ less, less." Remember how VAT was calculated: 5,600 rubles. – 118% X rub. – 18% In reverse proportion, the opposite is true. It contains “more-less”, “less-more” or vice versa “less-more”, “more-less”. I first came across the inverse proportion when I was doing calculations in connection with grain deliveries in hopper cars by rail (I had to do these calculations because the recipient accepted less goods than were sent). In a simplified way, my calculations can be represented as follows: The volume of goods supplied was supposed to be transported in batches of 10 wagons. But they discovered that it was 100 flights. How many cars must be added to each shipment to make 40 trips? 10 cars – 100 trips X cars – 40 trips X = 10*100/40 = 25 cars in each batch. That is, to 10 cars you need to add 15 more cars. Did you notice? We are no longer acting “cross to cross” but “in parallel”. And why? But because here, the more flights, the fewer cars and vice versa: “more-less”, “less-more”. It's simple. 10-100 25-40 And in direct proportion it would be 10-25 40-100 Let's formulate this problem differently: The carrying capacity of one hopper car is 65 tons. In total, 65,000 tons had to be transported. This volume was supposed to be transported in batches of 10 cars. But they discovered that it was 100 flights. How many cars must be added to each shipment to make 40 trips?
Here, it seems, it’s simpler: we divide 65,000 tons of the total weight of supplies by 65 tons of the carrying capacity of one car and find that it all fits into 1,000 cars. Then for 40 trips we will need 1000 / 40 = 25 cars. But how much easier it is to solve the same problem using the inverse proportion! And now I propose to train your intellect by solving problems. To begin with, let's take problems from Magnitsky arithmetic, since they surprisingly simply teach practical thinking when using fractions. Problem 1: On a hot day, 6 mowers drank a barrel of kvass in 8 hours. We need to find out how many mowers will drink the same keg of kvass in 3 hours. Solution to problem 1
Problem 2: One man will drink a kad in 14 days, and he and his wife will drink the same kad in 10 days, and you know, on how many days will his wife drink the same kad? Solution to problem 2
Task 3: Someone asked a certain teacher how many students you have, because I want to send my son to your school. The teacher replied: if as many more students come to me as I have, and half as many and a quarter and your son, then I will have 100 students. Solution to problem 3
Problem 4: In a household consisting of two residential buildings, there once lived a family consisting of two parents and three children, one son and two daughters. Initially, the household consisted of one house with an area of 62 sq.m. In 1978, the spouses divorced, and ownership of the old house was divided between them, with each spouse owning 1/2 of the old house.
After this, the father, using all possible help from his children, built a second house with an area of 124 sq.m. The house was built by 1985 and was listed as the property of the father.
Then the father gave 1/4 of this new house to the youngest of his daughters, who was a disabled person of the second group and was dependent on both parents, despite the dissolution of her parents’ marriage. After serving in the army, my son went to live in another city. The other, eldest daughter, who was not disabled, married her husband and her family lived in a new house with her father. This daughter had two children (grandchildren). The father died in 2007 and after him no one filed an application for inheritance.
The mother died in 2009, and after her death she left a will in which she bequeathed all her property to her son. The eldest daughter also died in 2009, 4 months after the death of her mother.
The son, who came from another city, filed an application for inheritance, and then went to court, demanding that his ownership of 4/6 in the old house and 1/4 in the new house be recognized. Are his demands legitimate and what is the maximum share he can claim? How should the shares be distributed among the heirs? At the time of the dispute, the old house was valued at 585,000 rubles, and the new one at 1,738,000 rubles. Solution to problem 4
Problem 5: In 2000, the testator, who owned 1/2 share of a residential building, died. The other 1/2 share belonged to the testator's son. The deceased had a son and 4 daughters, one of whom died in 1999; the deceased was survived by a husband and two children. Another daughter is disabled, the disability was acquired while working in a “harmful” industry. The testator bequeathed her 1/2 share to her son.
The son of the testator and her disabled daughter approached the notary to enter into an inheritance.
6 months after the opening of the inheritance, the notary issued the son a certificate of the right to inheritance for 13/15 shares, and 2/15 shares went to the sister. The son-heir decided to challenge his sister’s inheritance, since she has two apartments, she never lived in the house and did not look after her mother. What are the prospects for this dispute and what should happen as a result? Solution to problem 5
Task 6: The tax inspectorate, as a result of an inspection of a taxpayer who is on the general taxation system, established that the taxpayer purchased hot-rolled sheets 08Х18Н10Т, the size of one sheet is 0.6x1000x2570 mm, the total weight is 4.365 tons. For the purchase of all this steel, the supplier was paid 401,567.72 rubles for the entire batch, including VAT - 61,256.09 rubles. At the same time, it was established that 156 sheets of the specified steel were sold; accordingly, the taxpayer had to pay VAT at a rate of 18% of the price sold.
The metal sold according to invoices was sold at a price of 1,770 rubles per sheet of metal, including VAT (included in the indicated price). The tax inspectorate calculated that the VAT payable to the budget is 45,120 rubles. Is this amount determined correctly? The density of steel in this case is 7295.7 kg/m3. Density is calculated by dividing the mass by the volume, as can be seen from the “kg/m3” indicator.
Solution to problem 6
Law on the sale of shares in real estate
On January 2, 2021, amendments to Federal Law No. 218-FZ “On State Registration of Real Estate” came into force. The law separately regulates new rules for the sale of shared ownership.
- Allocating a share in an apartment is impossible if its size does not allow the owner to fully live in the allocated area. The law establishes an accounting minimum for living with all amenities. If the share does not reach this standard, it will not be possible to sell it;
- Each region of the Russian Federation has its own norm for a separate share. Its footage, depending on the region, ranges from 8-15 square meters per participant. For Moscow, for example, the minimum norm is 10 sq.m.
The same rules apply for registration. Registration of a citizen is impossible if the size of his share does not reach the established norm.
An exception is allowed for relatives of the owner, but this aspect has not yet been approved. The apartment can no longer be divided into an indefinite number of owners.
It can be divided into shares as a percentage based on the minimum size of the share area.
Please note that the bill only provides for cases of sale of a share of property. If we are talking about the allocation of a share during privatization, inheritance or division of property during divorce, it does not apply to these situations. It should be noted that some provisions of this law will not take effect until January 1, 2021.
Step-by-step instructions for allocating a share in court
A person who is faced with housing disputes for the first time most often has no idea where to start. We have prepared step-by-step instructions for you, which are designed to simplify the procedure for establishing the right to a share of property.
- The first thing you need to do is decide why you need the allocation. Then you will decide whether you want to allocate a portion in kind or in monetary terms.
- Next, you need to understand whether it is technically possible to isolate a part in kind, or you will have to be content with money; what kind of allocation options are generally possible in this case; how many shares will there be and what size are they; how much your part of the property will cost on the real estate market. The answers to these questions will be given by an expert assessment.
- Once you have decided why you need the allocation, you need to try to discuss it with other owners of the premises. If you managed to agree and sign a share agreement, then the main process is completed. And if not, then move on.
- Drawing up a statement of claim, preparing a package of documents, calculating the amount of state duty and paying it.
- Submitting a statement of claim and documents to the court. Beginning of the case and court hearings.
- Receipt of a court decision that has entered into force.
- Registration of changes in Rosreestr and BTI.
If the court decision contains even the slightest change in the ratio of shares and ownership, then each owner must record this with government agencies.
Statement of claim
Drawing up a statement of claim will not be difficult if you have all the necessary information about the owners and the property. You can submit statements of claim and simply fill them out. For example, the Garant website presents a large library of samples. The application must contain the following information:
- name and address of the court to which the claim is filed;
- personal information of all owners and participants in the case;
- detailed information about the property: address, total area, number of rooms, number of owners;
- title documents for the apartment;
- an indication of pre-trial means of resolving the dispute;
- data on expert assessments;
- list of attached documents;
- date;
- plaintiff's signature with transcript.
A package of documents that must be attached to the statement of claim: the plaintiff’s passport details, an extract from the Unified State Register of Real Estate, confirmation of rights to own real estate, a receipt for payment of the state duty. The number of copies of the claim must correspond to the number of owners.
The consideration of the case in court will take from two to six months. But the legal process itself is not all the time that may be needed for the judicial allocation of a share. It will take time for examination and assessment, for studying the statement of claim, pre-trial hearings, directly for court hearings, as well as for a possible appeal of the court decision.